RL Skating | Brennen A. Hill

Abstract

We present a framework for training a quadruped robot to roller skate using deep reinforcement learning (RL). To overcome the target hardware’s (Unitree Go1) lack of leg yaw, we introduce a novel passive wheel design called the “X configuration”, which enables the conversion of sideways leg motion into forward propulsion. Training is conducted using a massively parallel RL framework in the Isaac Gym simulator. The trained policy discovers complex and emergent gaits, automatically switching from a diagonal gait at 1 m/s to a galloping gait to achieve 3 m/s. We demonstrate that this learned roller-skating locomotion is significantly more energy-efficient than a traditional trotting gait, exhibiting a substantially lower cost of transport and mechanical power at equivalent speeds. This research validates passive roller skating as a viable, low-cost, and highly efficient locomotion strategy for legged robots.

I. Introduction

A. Motivation

Energy efficiency remains a critical challenge in legged robotics. While legged robots offer unparalleled all-terrain mobility, their modes of locomotion, such as trotting or walking, are often energetically expensive. One promising solution is hybrid wheeled-legged robots, but existing designs frequently rely on actuated wheels, which add significant cost, complexity, and weight to the system.

This project explores an alternative: equipping a quadruped robot with passive, unactuated roller skates. This approach maintains the low cost and mechanical simplicity of a purely legged system while offering the potential for high energy efficiency on flat surfaces.

However, controlling such a system is highly non-trivial. The dynamics of roller skating, generating forward motion from sideways leg pushes, are complex and difficult to model or hand-engineer. We turn to deep reinforcement learning (RL) as a data-driven approach to master this skill. By defining a suitable reward structure, RL allows the robot to discover optimal control policies and complex gaits automatically.

Our work is built upon legged_gym [1], a state-of-the-art RL codebase for legged locomotion. It leverages the NVIDIA Isaac Gym physics simulator, which enables massively parallel training of thousands of robots, allowing policies to be trained in minutes.

While legged_gym and similar frameworks have successfully trained robots to walk, run, and trot, our primary contribution lies in the behavior side. We adapt this framework to a novel hardware configuration: a Unitree Go1 quadruped modified with passive roller skates. This paper focuses on designing the system, developing the RL framework to train it, and analyzing the resulting emergent roller-skating behavior. This provides a new benchmark for energy-efficient locomotion, comparing it against both traditional trotting gaits and more complex actuated wheeled-legged robots.

C. Objectives

The primary objectives of this project are:

To design and implement a quadruped robot with passive wheels in simulation, including a novel wheel configuration to overcome the hardware’s mechanical constraints.
To develop a deep reinforcement learning framework, including observation spaces, action spaces, and a reward function, to train the robot to roller skate.
To demonstrate that the trained policy can achieve stable, high-speed locomotion and track varying velocity commands.
To analyze the emergent gaits discovered by the RL agent at different speeds.
To quantify and compare the energy efficiency of the learned roller-skating gait against a traditional trotting gait.

D. Overview of the Report

The remainder of this report is organized as follows. Section II provides a brief background on reinforcement learning in the context of this problem. Section III details our methodology, including the hardware setup, software architecture, and the design of the RL observation, action, and reward spaces. Section IV presents our results, including maximum achieved speeds, analysis of emergent gaits, and a quantitative comparison of energy efficiency. Section V discusses key implementation challenges, such as friction simulation, and limitations of the current work. Finally, Section VI concludes the report and suggests avenues for future research.

II. Background: Reinforcement Learning

Reinforcement Learning (RL) is a machine learning paradigm where an agent (the robot’s control policy) learns to interact with an environment (the physics simulation) to maximize a cumulative reward signal. At each timestep, the agent observes the environment’s current state $s_t$, takes an action $a_t$, and receives a scalar reward $r_t$ and the next state $s_{t+1}$. The goal is to learn a policy, $\pi(a_t\|s_t)$, which is a mapping from states to actions that optimizes the expected long-term return (sum of rewards). In this work, we use RL to discover the complex sequence of motor commands required to achieve stable and efficient roller skating, a task that would be exceptionally difficult to explicitly program.

III. Methodology

A. Hardware Setup

The robot used in this project is the Unitree Go1 quadruped. It features 12 motors, with 3 motors on each leg: a hip motor (roll), a thigh motor (pitch), and a calf motor (pitch).

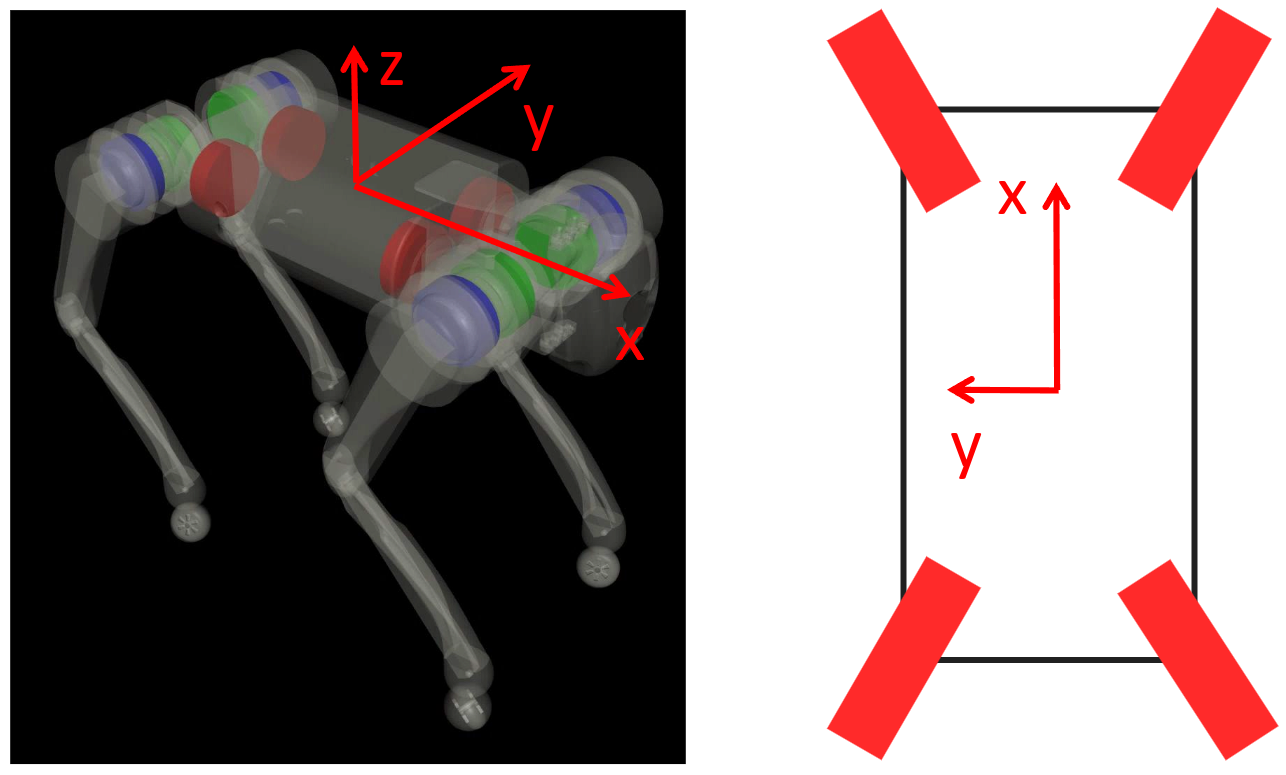
The key to human roller skating is the ability to rotate the foot (yaw) to couple sideways motion with forward motion. However, the Go1’s legs are mechanically constrained; they cannot yaw and are always parallel to the robot’s base x-axis.

To solve this, we designed a fixed “X Configuration” for the passive wheels. As shown in Fig. 1, each wheel is installed with a fixed 30-degree yaw angle relative to the body’s x-axis. This configuration is symmetric left-to-right and front-to-back, allowing sideways pushes from any leg to be converted into forward motion.

Fig 1. Left: Robot motor groups (red: hip/roll, green: thigh/pitch, blue: calf/pitch). Right: "X Configuration" of wheels, angled at 30 degrees from the body x-axis.

B. Software Setup

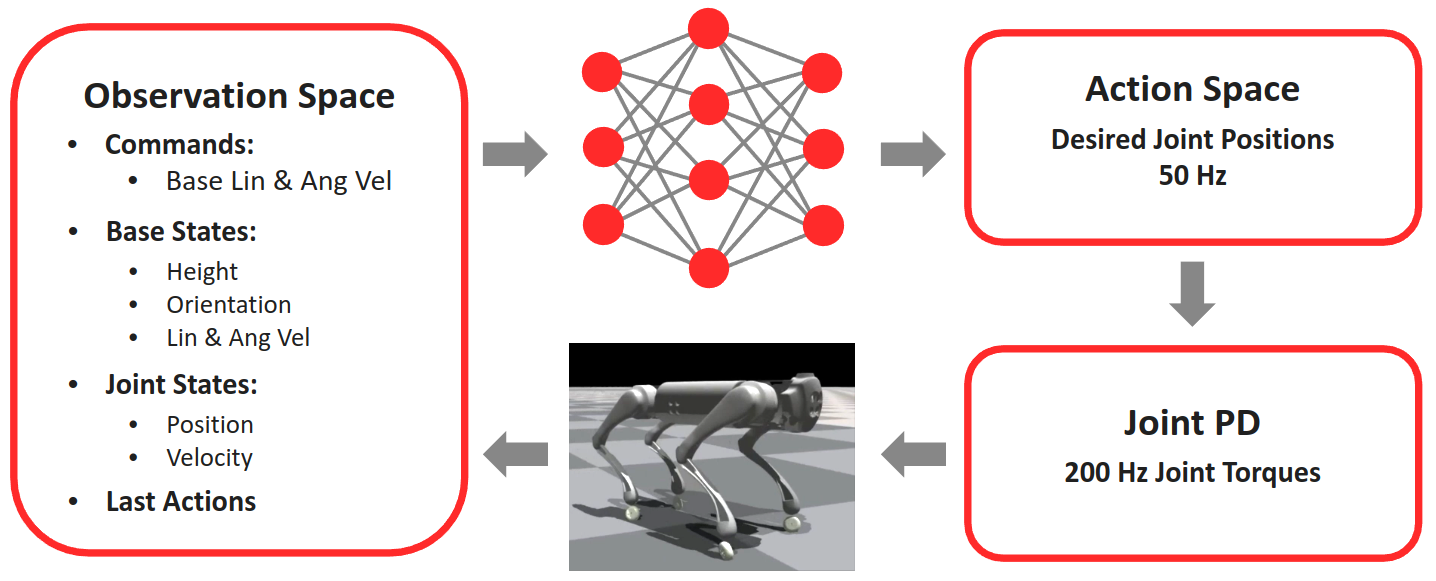
Our controller architecture is a hierarchical system, as shown in Fig. 2.

High-Level Policy: A neural network (the RL agent) runs at 50 Hz. It takes observations from the robot’s state (detailed in Sec. III-C) and outputs the desired joint positions for all 12 motors.
Low-Level Controller: A joint-level Proportional-Derivative (PD) controller runs at 200 Hz. It receives the desired joint positions $q^d$ from the policy and computes the necessary motor torques $\tau$ to achieve them.

Fig 2. Software Block Diagram. The high-level policy (neural network) runs at 50 Hz, outputting desired positions. A low-level PD controller runs at 200 Hz to compute joint torques.

C. Observation Space

The observation $o$ provided to the policy network includes:

Commands: Desired base linear velocity in the xy-plane ($^{\mathcal{B}}\mathbf{v}_{xy}^{d}$) and angular velocity around the z-axis ($^{\mathcal{B}}\omega_{z}^{d}$).
Base States: Base height, base orientation (represented as a “projected gravity” vector), and current base linear ($^{\mathcal{B}}\mathbf{v}$) and angular ($^{\mathcal{B}}\mathbf{\omega}$) velocities.
Joint States: The position $\mathbf{q}$ and velocity $\dot{\mathbf{q}}$ of all 12 motors.
Last Actions: The action $\mathbf{a}_{\text{prev}}$ taken in the previous timestep, which helps the policy learn smooth control.

D. Action Space and Low-Level Control

The action $\mathbf{a}$ outputted by the neural network is scaled to produce the desired joint positions $\mathbf{q}^d$. These are fed to the low-level PD controller, which calculates the final motor torques $\mathbf{\tau}$ using a zero desired joint velocity:

\[\mathbf{\tau} = k_{p}(\mathbf{q}^{d} - \mathbf{q}) - k_{d}\dot{\mathbf{q}}\]

where $\mathbf{q}$ and $\dot{\mathbf{q}}$ are the current joint positions and velocities, and $k_p$ and $k_d$ are the PD gains.

E. Rewards and Regularizations

The reward function is crucial for shaping the desired behavior. It is structured as a sum of tracking rewards, regularizations to encourage efficiency, and penalties to ensure physical constraints are met.

Tracking Rewards:
Base Linear Velocity (xy): $\exp(-\|^{\mathcal{B}}\mathbf{v}_{xy} - {^{\mathcal{B}}\mathbf{v}_{xy}^{d}}\|_{2}^{2} / \sigma)$
Base Angular Velocity (z): $\exp(-\|^{\mathcal{B}}\omega_{z} - {^{\mathcal{B}}\omega_{z}^{d}}\|_{2}^{2} / \sigma)$
Penalties (Negative Rewards):
Base Height: $-(z - z^d)^2$
Base Orientation: $-\|^{\mathcal{B}}\mathbf{u}_{g,xy}\|_{2}^{2}$ (penalizes tilt)
Base Linear Velocity (z): $-^{\mathcal{B}}v_z^2$ (minimizes hopping)
Base Angular Velocity (xy): $-\|^{\mathcal{B}}\mathbf{\omega}_{xy}\|_{2}^{2}$ (minimizes roll/pitch)
Collision Avoidance: $-\|\mathbf{f}\|_2^2$ (quadratic penalty on large collision forces on thigh/calf links)
Joint Position Limit: $-\|\mathbf{q}_{\text{exceed}}\|_2^2$ (penalizes exceeding joint limits)
Regularization:
Effort Minimization: $-\|\mathbf{a} - \mathbf{a}_{\text{prev}}\|_2^2$ (encourages smooth actions)
Heuristic: $-\|\mathbf{p}_{\text{vert leg, xy}}\|_2^2$ (vertical virtual leg regularization)

To promote a robust policy, we also employ domain randomization by adding noise to all observations and randomizing link friction coefficients during training.

IV. Results and Analysis

A. Command Range

After training, the robot was able to successfully track a wide range of velocity commands. The maximum command ranges we achieved are:

Forward Velocity ($v_x$): 3 m/s
Sideways Velocity ($v_y$): 2 m/s
Yaw Velocity ($\omega_z$): 3 rad/s

B. Automatic Gait Switch

A significant finding is that the RL policy learned to automatically switch its gait based on the commanded forward velocity, without any explicit instruction to do so.

At 1 m/s: Diagonal Gait When commanded to move at 1 m/s, the robot adopted a diagonal gait. In this gait, the robot keeps a diagonal pair of wheels (e.g., front-left and back-right) on the ground at the same time for stability. As seen in Figs. 3 and 4, the legs push sideways, and the “X configuration” of the wheels converts this push into forward motion.

Figs 3 & 4. The robot using a diagonal gait at $t_0$ (left) and $t_1$ (right). The legs push sideways to generate forward motion.

At 3 m/s: Galloping Gait When commanded to move at a higher speed of 3 m/s, the robot learned that the diagonal gait was insufficient. It autonomously developed a galloping gait. This gait is more dynamic, characterized by having only one wheel in contact with the ground at any given time. This gait involves more extreme side-to-side leg movements and appears similar to a horse’s gallop, enabling the robot to achieve greater speeds.

Figs 5 & 6. The robot using a galloping gait at $t_0$ (left) and $t_1$ (right). This more dynamic gait is used to achieve higher speeds.

This emergent behavior highlights the power of RL to discover complex and effective solutions in high-dimensional control problems.

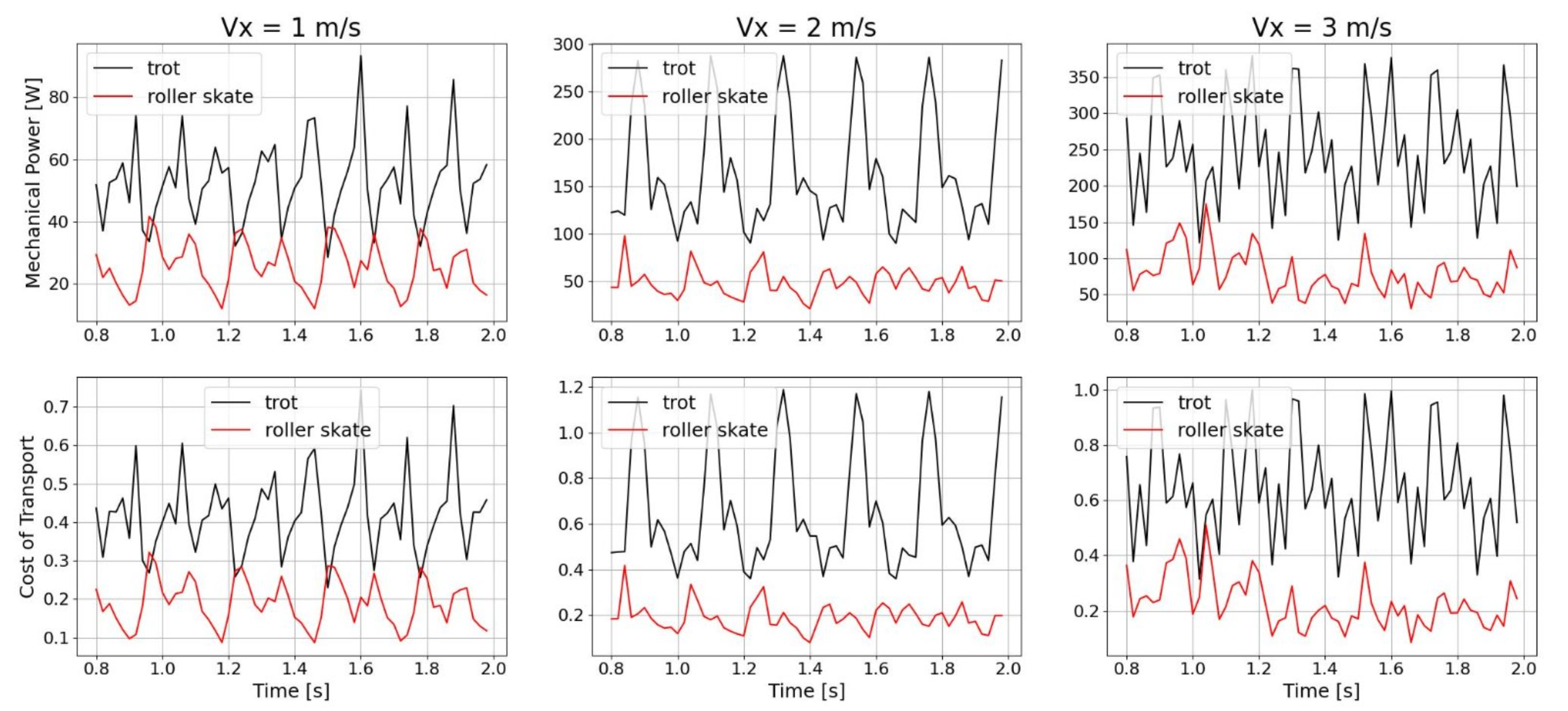
C. Energy Efficiency Comparison

To validate our primary motivation, we compared the energy efficiency of our roller-skating robot against a baseline trotting gait (where the robot steps without wheels rolling). We compared two key metrics:

Mechanical Power ($p$): Defined as the sum of absolute joint power. We use the absolute value as both positive and negative power draw from the battery (representing electricity consumption).
\[p = \sum_{i=1}^{n\_j} |\tau_i \dot{q}_i|\]
Cost of Transport (CoT): A normalized metric for efficiency.
\[CoT = \frac{p}{mg||\mathbf{v}_{xy}||_2}\]

The results, shown in Fig. 7, are conclusive. At all tested forward velocities (1 m/s, 2 m/s, and 3 m/s), the roller-skating gait (red line) is significantly more energy-efficient than the trotting gait (black line). Both the peak and average mechanical power and cost of transport are substantially lower when skating.

Fig 7. Energy efficiency comparison between roller skating (red) and trotting (black) at 1 m/s, 2 m/s, and 3 m/s. Top row: Mechanical Power [W]. Bottom row: Cost of Transport. Roller skating is significantly more efficient in all cases.

V. Discussion and Limitations

A. Friction Simulation

A major technical challenge arose during simulation. Initially, after adding rollers, the robot refused to skate and instead learned to trot, as if the wheels were not present. We discovered this was due to improper simulation of rolling friction in Isaac Gym. The simulator greatly exaggerates rolling friction when the wheel’s collision geometry is not an ideal sphere. We tested several geometries:

Wheel Mesh: Failed. The mesh was not a perfect circular object.
Cylinder: Failed. Isaac Gym converts cylinders to meshes for simulation, leading to the same issue.
Sphere: Succeeded. Using a sphere as the collision geometry for the wheel resulted in realistic rolling friction and enabled the skating behavior to be learned.

B. Whole Body Engagement

A limitation of our current reward function is that tracking rewards are applied only to the robot’s base, not its whole body. This can lead to a phenomenon where the robot tilts its entire body slightly to one side while keeping its base perfectly horizontal to satisfy the reward function.

A potential solution for future work is to incorporate whole-body level rewards, such as tracking the centroidal linear and angular momentum [2] or the center-of-mass position and whole-body orientation [3].

VI. Conclusion

In this project, we successfully demonstrated that a quadruped robot can be trained to roller skate using deep reinforcement learning. By designing a novel “X configuration” for passive wheels, we overcame the hardware limitations of the Unitree Go1 robot and enabled it to convert sideways leg motion into forward propulsion.

Our RL agent, trained in the legged_gym simulator [1], learned to locomote at speeds up to 3 m/s and developed complex, emergent gaits, automatically switching from a diagonal gait at low speeds to a galloping gait at higher speeds. Furthermore, our analysis shows that this roller-skating gait is significantly more energy-efficient than traditional trotting, as measured by both mechanical power and cost of transport.

We also identified and solved key simulation challenges related to rolling friction and identified limitations in our current reward function that can lead to whole-body tilt, suggesting clear avenues for future work. This work validates passive roller skating as a viable, low-cost, and highly efficient locomotion strategy for legged robots.

References

[1] N. Rudin, D. Hoeller, P. Reist, and M. Hutter, “Learning to walk in minutes using massively parallel deep reinforcement learning,” in Conference on Robot Learning. PMLR, 2022, pp. 91-100.

[2] H. Dai, A. Valenzuela, and R. Tedrake, “Whole-body motion planning with centroidal dynamics and full kinematics,” in 2014 IEEE-RAS International Conference on Humanoid Robots. IEEE, 2014, pp. 295-302.

[3] Y.-M. Chen, G. Nelson, R. Griffin, M. Posa, and J. Pratt, “Angular center of mass for humanoid robots,” arXiv preprint arXiv:2210.08111, 2022.